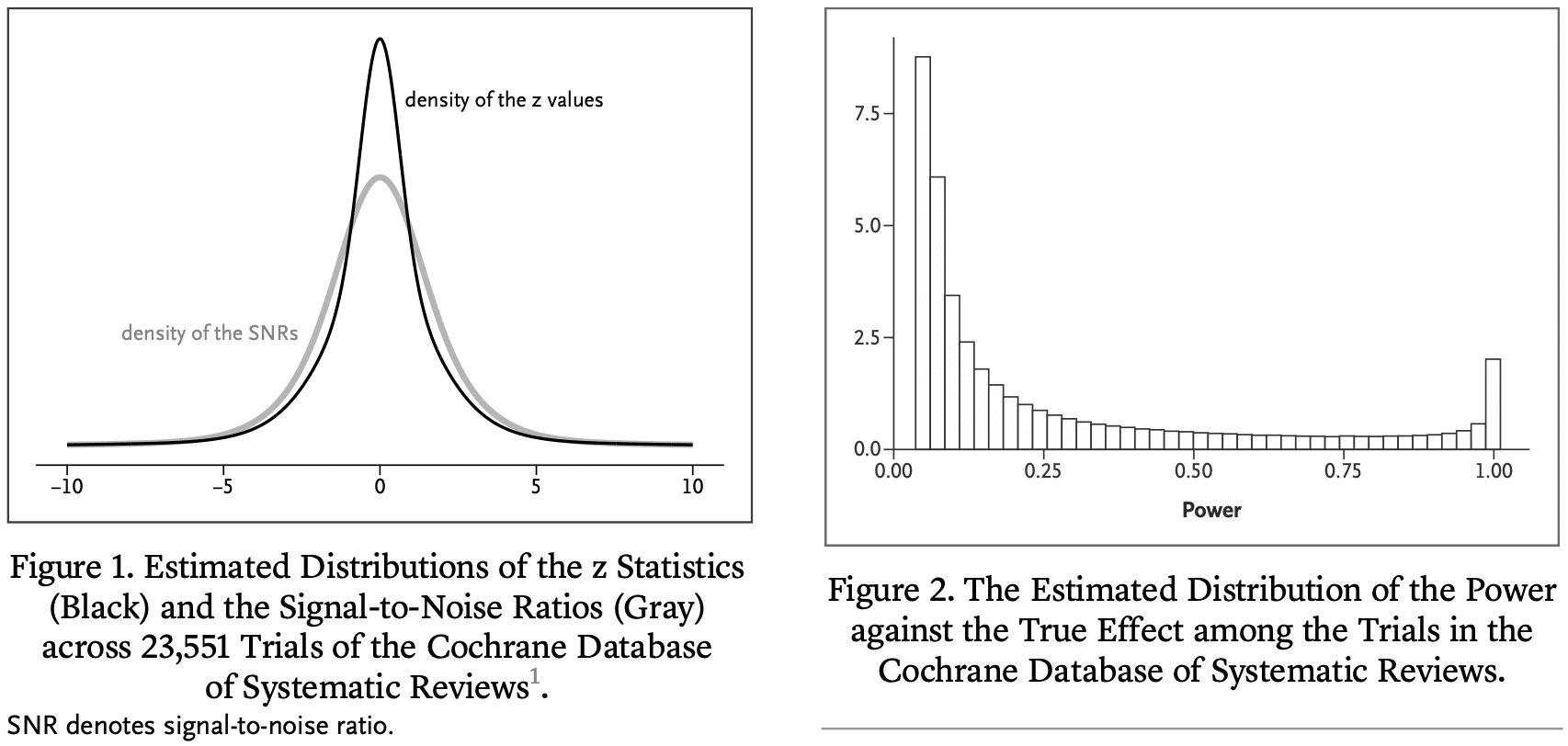
Erik van Zwet, Sander Greenland, Guido Imbens, Simon Schwab, Steve Goodman, and I write:
We have examined the primary efficacy results of 23,551 randomized clinical trials from the Cochrane Database of Systematic Reviews.
We estimate that the great majority of trials have much lower statistical power for actual effects than the 80 or 90% for the stated effect sizes. Consequently, “statistically significant” estimates tend to seriously overestimate actual treatment effects, “nonsignificant” results often correspond to important effects, and efforts to replicate often fail to achieve “significance” and may even appear to contradict initial results. To address these issues, we reinterpret the P value in terms of a reference population of studies that are, or could have been, in the Cochrane Database.
This leads to an empirical guide for the interpretation of an observed P value from a “typical” clinical trial in terms of the degree of overestimation of the reported effect, the probability of the effect’s sign being wrong, and the predictive power of the trial.
Such an interpretation provides additional insight about the effect under study and can guard medical researchers against naive interpretations of the P value and overoptimistic effect sizes. Because many research fields suffer from low power, our results are also relevant outside the medical domain.
Also this new paper from Zwet with Lu Tian and Rob Tibshirani:
Evaluating a shrinkage estimator for the treatment effect in clinical trials
The main objective of most clinical trials is to estimate the effect of some treatment compared to a control condition. We define the signal-to-noise ratio (SNR) as the ratio of the true treatment effect to the SE of its estimate. In a previous publication in this journal, we estimated the distribution of the SNR among the clinical trials in the Cochrane Database of Systematic Reviews (CDSR). We found that the SNR is often low, which implies that the power against the true effect is also low in many trials. Here we use the fact that the CDSR is a collection of meta-analyses to quantitatively assess the consequences. Among trials that have reached statistical significance we find considerable overoptimism of the usual unbiased estimator and under-coverage of the associated confidence interval. Previously, we have proposed a novel shrinkage estimator to address this “winner’s curse.” We compare the performance of our shrinkage estimator to the usual unbiased estimator in terms of the root mean squared error, the coverage and the bias of the magnitude. We find superior performance of the shrinkage estimator both conditionally and unconditionally on statistical significance.
Let me just repeat that last sentence:
We find superior performance of the shrinkage estimator both conditionally and unconditionally on statistical significance.
From a Bayesian standpoint, this is no surprise. Bayes is optimal if you average over the prior distribution and can be reasonable if averaging over something close to the prior. Especially reasonable in comparison to naive unregularized estimates (as here).
Erik summarizes:
We’ve determined how much we gain (on average over the Cochrane Database) by using our shrinkage estimator. It turns out to be about a factor 2 more efficient (in terms of the MSE) than the unbiased estimator. That’s roughly like doubling the sample size! We’re using similar methods as our forthcoming paper about meta-analysis with a single trial.
People sometimes ask me how I’ve changed as a statistician over the years. One answer I’ve given is that I’ve gradually become more Bayesian. I started out as a skeptic, concerned about Bayesian methods at all; then in grad school I started using Bayesian statistics in applications and realizing it could solve some problems for me; when writing BDA and ARM, still having the Bayesian cringe and using flat priors as much as possible, or not talking about priors at all; then with Aleks, Sophia, and others moving toward weakly informative priors; eventually under the influence of Erik and others trying to use direct prior information. At this point I’ve pretty much gone full Lindley.
Just as a comparison to where my colleagues and I are now, check out my response in 2008 to a question from Sanjay Kaul about how to specify a prior distribution for a clinical trial. I wrote:
I suppose the best prior distribution would be based on a multilevel model (whether implicit or explicit) based on other, similar experiments. A noninformative prior could be ok but I prefer something weakly informative to avoid your inferences being unduly affected by extremely unrealistic possibilities in the tail of the distribuiton.
Nothing wrong with this advice, exactly, but I was still leaning in the direction of noninformativeness in a way that I would not anymore. Sander Greenland replied at the time with a recommendation to use direct prior information. (And, just for fun, here’s a discussion from 2014 on a topic where Sander and I disagree.)
Erik concludes:
I really think it’s kind of irresponsible now not to use the information from all those thousands of medical trials that came before. Is that very radical?
That last question reminds me of our paper from 2008, Bayes: Radical, Liberal, or Conservative?
P.S. Also this:
You can click through to see the whole story.
>>> Read full article>>>
Copyright for syndicated content belongs to the linked Source : Hacker News – https://statmodeling.stat.columbia.edu/2023/12/23/bayesians-moving-from-defense-to-offense-i-really-think-its-kind-of-irresponsible-now-not-to-use-the-information-from-all-those-thousands-of-medical-trials-that-came-before-is-that-very/
